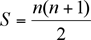Solutions to ProjectEuler.net

Solution

233,168

Explanation

The easiest way to solve this problem is by Brute Force . This can be achieved by running a loop beginning at 1 and incrementing by 1 until 1000. In each iteration we check if the current number is divisible by 3 or 5. If it is, we add it to our sum otherwise continue to increment. Once the loop terminates we have our sum. We can generalize this idea simply checking for divisions by other factors and looping until we've reached out desired upper limit. The advantage to the Brute Force method is that it is very easy to translate into code.

A second clever appraoch is to employ the Gauss Sum Formula.The formula allows us to sum a series of numbers with the pattern 1 + 2 + 3 + ... + n, where n is the upper limit. The Gauss Formula is as follows,

Thus, we can easliy compute the sum. Now you may be wondering how can we use this formuala to our advantage? Well let's use some algebra to help us. Using Problem 1 as our example, let's consider all numbers factorable by 3. We can quickly determine we will have to sum 3 + 6 + 9 + 12 + ... until we reach 999. If we divide this series by 3 we can rewrite it as 3*(1 + 2 + 3 + ... + 333). Hey, there's the pattern that fits the Gauss Sum Formula! We can do the same for factors of 5. Now, the only thing we have to be careful about is double counting. For instance 15, 30, 45, and so forth are divisible by 3 and 5. In out calculations we'll have to make sure each value is only counted once. We should now be able to solve this problem much faster than the Brute Force method. The downside is that this method is more challenging to generalize in code.